Fény hullám a víz sodrásában  

  

 

A fénynek az a furcsa tulajdonsága, hogy iránya megtörik ha ferdén halad át sűrűbb közegből a ritkába. Vagy éppen fordítva halad át a sűrűbbe ezt fénytörésnek nevezzük, ami valójában igen triviális elnevezés. A ritkább közeg helyesen szólva optikailag ritkább közeg, a sűrűbb pedig optikailag vett sűrűbb közeg. Ezért itt nem a közeg sűrűségéről (fajsúlyáról) beszélünk, hanem itt a közeg valamilyen mélyebb tulajdonságáról van szó.

 

   A fénytörésnél belépő és kilépő szögek szinuszáról van szó, de szemléletesebb az ezzel arányos fénysebességben gondolkodni. A vákuum törés mutatója n₀=1, a levegőé n_lev=1,003, a víz törés mutatója n_víz=1,33, a gyémánté n_gy=2,2. Az n számok megmutatják, hogy hányszor lassabban halad a fény az illető közegben mint a vákuumban. A átszámítás bázisa a fénysebessége a vákuumban, amely nagy pontossággal kiszámított érték, c=299. 792.458. m/s. Így tehát a vízben a fény c/1,33= 225...000...000...m/s. A fény tehát lassabban halad a vízben mint a vákuumban, de vajon miért?

 

 

  Amikor a víz áll  

 

 

   A víz belseje számos titkot is takar. Gondoljunk egy vízszintesen elhelyezett üvegcsőre a vákuumban, melyet vízzel feltöltöttünk és végeit átlátszó lemezkékkel lezártuk. A cső felett és alatt, valamint előtt és után a fényhullámok sebessége természetesen c. Az üvegcsőben azaz a  vízben kisebb mint c, mégpedig az előbb kiszámolt c_víz értékre módosult:         

 

0.) cvíz=c/n. 

 

   A kérdés az, hogy a vízben lassabban haladó hullámok sűrűsége és magassága megváltozik-e? Igen, megváltozik, ahogy azt az 1 ábra mutatja.

 

  

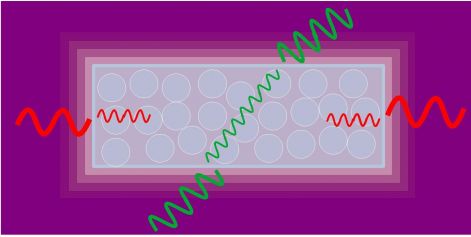
1. ábra fényhullámok változása vízben

 

     A cső körül igen sűrű, és igen nagy energiájú de teljesen átlátszó anyag a vákuum van.  Ez ugyan teljességgel láthatatlan és színtelen, de az ábrán lila színnel jelöltük. A vákuum behatol az üvegcső belsejébe, sőt behatol víz atomjaiba is. Az atomoknak az a különleges tulajdonsága, hogy  intenzíven nyelik az energiát, ebből tartják fenn magukat, majd  észrevétlenül elküldik azt  valahova- talán a hipertérbe. Az atomok már csak ilyenek! (Bővebben lásd itt!)

 

    A vízben a vákuum energiája 1 n jelűtörésmutatóval csökken.  Ennek következtében mind az megváltozott energiáját, mind a sebességét 1/n szorzó, vagy is 1/1,33szorzó használatával kapjuk meg. A vízben lévő vákuum tehát csökkentet energiával és csökkentett sebességgel hajtja előre a fényt.   Az  1/1,33 arányában csökken a fényhullám hossza, és a hullámok magaságga is.  A vízben haladó  a hullámok tehát arányosak a vákuumbeli hullámokkal, csakhogy 1,33szor kisebbek.

 

   Nyilván felvetődik bennünk, hogy hová lesz a nagyobb hullám energia-tartalma ha a mérete kisebbé válik. Az bizony elvész, az energia különbséget felveszi a víz. És mi, lesz akkor, amikor a kisebb hullám kilép a vízből, és nagyobb hullámként kell  tovább haladni? Az fog történi, hogy a vákuum azonnal kellő mennyiségű energiát ad át a fényhullámnak. A vákuum nem türi el, hogy egy adott frekvenciájú fényhullám kisebb hullámhosszúságú, kisebb amplitúdójú, kisebb sebességű és kisebb energiájú legyen mint amit az ő energia állapota diktál.

 

     A víz és egyéb átlátszó közegek törésmutatóját könnyű megmérni, egy ferde fénysugár és egy szögmérő kell hozzá. Egy üvegedénybe belel öntik az optikailag sűrűbb közeget ferdén bele vezetnek egy fénysugarat, amely belépéskor megtörik és a szögek arányából vissza számolható a törésmutató.

 

   Az ábrán látható nyilak hossza mutatják nekünk a hullámok sebességét: a belépő hullám nagyobb sebességű, a vízben haladó hullám kisebb sebességű, míg a vákuumba kijutó hullám ismét nagy sebességű lesz.

 

   A helyi energia állapotokat pedig az E betűk nagysága mutatja. Az ábrán a helyi energiák nagyobb e betű jelöli, míg a 0 index az energia alapállapotára utal. A vízben az energiája az n törésmutatóval arányosan kisebb, ezért az E_víz jelölés is kisebb. 

 

   A fenti kísérlet megállapításai a mindennapi élet is igazolja, amikor ránézünk a kettős ablaküvegen áthatoló fénysugárra. A napsugár a levegőben halad, közel vákuumbeli sebességgel. Amikor behatol a külső üveg táblába, akkor lelassul, mert az üvegtörés mutatója közel van a víz törésmutatójához. Kilépés után újra felgyorsul, belső üvegtáblába újra lelassul, majd kilépve újra felgyorsul. Ezt az ismételt sebesség- számot tovább is növelhetjük, ha további üvegtáblákat teszünk a fénysugár útjába.

 

 

  Amikor a víz mozog  

 

 

Jó készüléket szerkeszteni, és az optikailag sűrű közeget nagy sebességgel mozgatni bizony nehéz dolog, nem sok ilyen kísérletet végeztek el.

 

   A w sebességet Zeeman kísérleti fizikus nagy pontossággal megmérte, mert sikerült neki egy üveghasábot nagy sebességgel mozgatni. A finomra csiszolt üveghasábot kis ágyúból lőtte ki, így kis túlzással azt mondhatjuk, hogy a hasáb egy ágyúgolyó sebességével repült. Közben a megosztott egyik fénysugár egyik ágát át vezette az üveghasábon, míg a másik ágát mellette, a levegőben küldte el a megfigyelőpont irányba. 

 

  

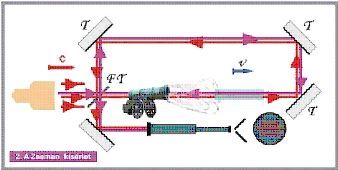
2. ábra a Zeeman kísérlet

 

   A különböző mérések alapján felállított egy tapasztalati képletet a w kiszámításához: 1.)    w=c/n + v/n²

 

  A képlet ugyan jó csak azt nem lehet tudni, hogy miért pont ilyen. Mondhatnánk, hogy Mert csak!   Vagy mondhatnánk azt is, hogy a természet már csak ilyen.

 

   A képlet levezetése  

 

Az alábbiakban megpróbálom a képlet fizikai tartalmát is feltárni.

 

   Természetesen azt gondoljuk, hogy  a mozgó üveghasábon átvezetett fényt a közeg magával sodorja, és így a mozgás sebességével gyorsabban halad a fény. Ez az elgondolás  képletben így írható fel:    

 

2.) w'=c/n +v

 

   ahol w' a fény megváltozott sebessége és v az üveghasáb sebessége.

 

   Azonban ez a képlet ebben a formában nem jó. A fenti képlet csak akkor lenne igaz, ha a folyadékba, azaz a vízbe nem hatolna be az éter és nem lenne jelentős hatással a mozgó fényre és a mozgó vízatomokra, illetve az üveghasáb atomjaira.

 

   Hatás szempontjából a víz csak kétharmad részben tölti meg az üvegcsövet, mert  az álló aether hatása is érvényesül egyharmad részben.( Lásd az 1 ábrát ismételten.). Ennek következtében a hozzáadott sebesség nem v lesz, hanem v/n.

 

   Tehát a képlet második tagjában is belép a törésmutató, amely lecsökkenti a  magával ragadás sebességét. Az eddig el mondottak képlet formájában így néznek ki: 

 

  

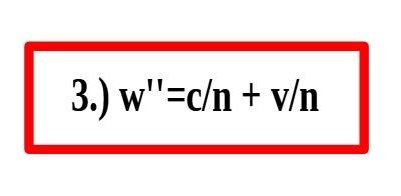
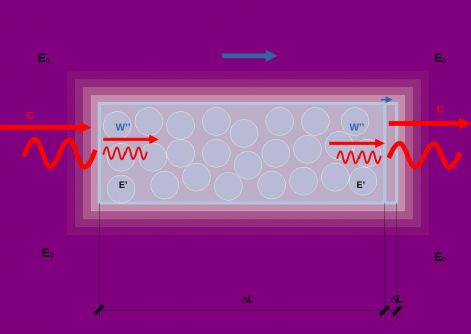
3. ábra   A Zeeman kísérlet elméleti bemutatása

 

   A 3 ábra újra mutatja a Zeeman kísérletet egy kis változással, de elméleti vonatkozásban fontos többlettel. Persze csak a fény számára tűnik megnyúltnak, mert a v sebesség miatt hosszabb utat kell megtennie. Ez a többet út az üveghasáb orrán (elején) látszik, mintha az üveghasáb picit megnyúlt volna. Ha a fényhullám útját három részre bontjuk, akkor az első fázis az a pillanat, amikor a fényhullám hátulról eléri a hasábot és kezd belehatolni. A második fázis az amikor a fényhullám az  L hosszúságú mozgó üveghasábban halad keresztül. Az erre fordított idő: t=L/w’’. Mire a fényhullám elérné a mozgó hasáb elejét, addigra az bizony már előrébb mozdult DL=w’’*t értékel. Ez többlet utat és többlet időt jelent a vákuumbeli mozgáshoz képest. Ennek valahogyan meg kell jelenie a képletben, amit a második tag újabb 1/n szorzásával hozhatunk létre. Ez a végső képlet második tagjában 1/n² alakot jelent és így tovább csökkenti a magával ragadás mértékét. Ezzel a szorzással tehát vissza kaptuk Zeeman 1. számmal jelölt kísérleti eredményét:

 

4.) w=c/n + v/n²

 

   Egyértelműen látszik, hogy a hivatkozott elméleti képlet megegyezik  Zeeman kísérlet útján kapott 1. számú képletével. A fenti kis optikai levezetésem azonban nem tesz elbizakodottá.

 

   A korabeli tudósok sok pontos optikai mérést leközöltek, valamelyik szakmai könyvtárban nyílván ott porosodik néhány vaskos kötet, amelyben bizonyára el van rejtve a fenti levezetés. Talán annyi érdemem van, hogy felfrissítve újra bemutatom a kősodorból jelenleg kikerült, ámde mégis nagyon értékes témát.

 

   Ha jól meggondoljunk, akkor Zeeman 1. számú képlete a fény magában ragadásán kívül egy másik fizikai effektust is rejt magában. Jelesül azt, hogy a fény kilép az egyik optikai rendszerből, az üveghasábból, és átlép egy másik közegbe, a vákuumba. Közben beszámítódik a képletbe egy trükkös átlépési effektus. Így tehát a fény korrekt magával ragadási a 3. számú képlet: W”=c/n+v/n. Van azonban az efféle kísérleteknek egy másik fajtája, ahol a fénynek nem szükséges átlépkednie egy másik közegbe, hanem megmaradhat a mozgó vízben és így közvetlenül megadja a helyes 3. jelű  magával ragadási képletet. Ilyen volt például a francia Fizeau kísérlete. (Részletesebben lásd itt!)

 

   Utószóként had mondjak el egy-két záró gondolatot a fenti témához, vagy méginkább a fény általános természetéhez. Ezek biztosan nincsenek benne az alaposan kidolgozott német szakkönyvekben. Az egyik az, hogy a fény megismerésének útján még nagyon az elején járunk. A fény problémájának megoldása még gyermek cipőben jár. Az meg pláne messze van, hogy véglegesre felépüljön a fényből készült gyönyörű szép kristálypalota. Jómagam, 3 téglát is megpróbáltam hozzá tenni az építéshez. (Bővebben lásd itt, itt és itt!) Szerintem ez még mindig édes kevés, ezért teszek majd egy kísérletet az eddigi vélemények, és a saját többlet-gondolataim összefoglalására, illetve egyeztetésére. Talán előre viszi az optika tudományát.

 

Vegyük észre, hogy a fény és környéke tele van hiányokkal, megmagyarázatlan dolgokkal és tévedésekkel! Ez azért van, mert a fizikából hiányzik az anyagi dolgokat összekötő közvetítő anyag, az aether. Ez a dolgozat is világosan mutatja, hogy már ezek az egyszerű kísérletek sem magyarázzhatók meg az éter nélkül. Éter nélkül a természet nem működik! -mondotta Einstein egy BBC előadáson (1923). Ugyan csak ő volt az, aki élete alkonyán ezt írta egy életrajzi művében:"Egész életemben azon fáradoztam, hogy megoldjam a fénykörüli problémákat. Sajnos nem sikerült előre lépni." 

 

Kelt: 2022. Március 15

 

Tassi Tamás 

Gépészmérnök 

Hobbi- Fizikus 

aparadox.hupont.hu

 

 

 

 

 

 

 

Kulcsszavak: Fény, Optika kísérletek, Zeeman, Fizeau,

 

 

 

 

 

 

 

 

 

 

Oldal: Fényhullám a vízsodrásában
A Zöld Csillag - © 2008 - 2024 - a-zold-csillag.hupont.hu

Az ingyenes honlapkészítés azt jelenti, hogy Ön készíti el a honlapját! Ingyen adjunk: Ingyen Honlap!

ÁSZF | Adatvédelmi Nyilatkozat